８月１週

ようこそ！生まれいずるシナプス
８月２日（火）雨　書斎テラス、蜘蛛の巣の雨粒

ギリギリと締め付ける音が聴こえる。
どうして今までこの音が３次元の子宮収縮の音であり、子宮の海に漂っているのが自らだと気付かなかったのだろう？
老化することによって活動の量と質が低下し、躍動領域が狭められ、存在の意味を徐々に失う。
この背後に常に流れていた通奏低音こそ、３次元子宮収縮の奏でる葬送の調べだったのだ。

となると今為すべきことは、この穏やかな子宮の海から異次元・黄泉へと脱出すべく、
頭頂骨２枚と前頭骨２枚、計４枚の頭蓋骨を重ね合わせ、可能な限り頭部を小さくすることなのでは！

*西畑への散水管を地中に*	*大泉門* 問題は４枚の頭蓋骨を重ねるための大泉門を形成出来るか否かにある。胎児はこの大泉門に４枚の頭蓋骨を重ね合わせ、最大の肉体パーツである頭部を最小にして、新たな世界へ脱出する。	*ゲートのコンクリート剥がし*
しかしこの大泉門は生後２年程で完全に閉じられ、再び開くことはない。２つの世界を結ぶこの大泉門が、位相空間学の４次元帽子と云われた境界も表裏の区別も持たない曲面のクライン体であると幻想したのは、位相空間学を	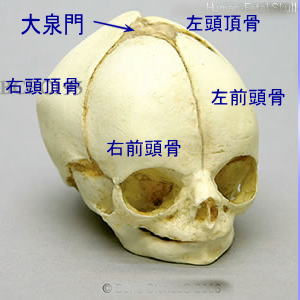*Anterior Fontanel*	学び始めた大学２年だったろうか？２次曲面には裏表があり、境界を超えない限り反対側に行くことは出来ない。この境界を部分的に繋げて円柱を作ると、円柱の内と外が出来るが一度捩じって繋げると表裏一体のメビウスの帯が出来る。
*この管を地中に埋設*	円柱の残りの境界を繋げるとトーラスと呼ばれるドーナツとなり、内と外に分けられる閉鎖空間が出来る。一方メビウスの帯の境界を繋げると内と外が繋がった曲面のクライン体が作れると知って、何とか繋げられないかと各種のモデルを作り、１年間試行錯誤した事があった。	*これなら車が乗っても潰れない*

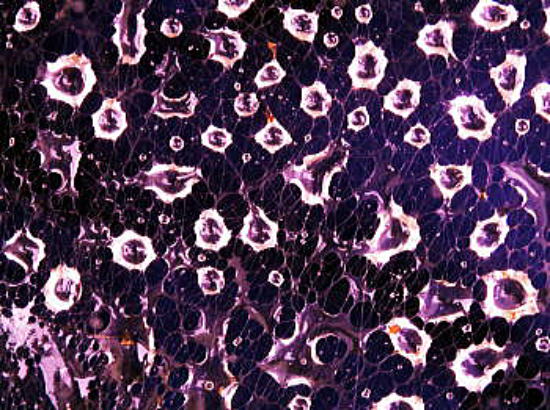蜘蛛の巣に絡めとられた銀河

その試みの過程で得た唯一のものが
位相空間と相いれない、大泉門と
４次元の十字帽子の視覚的類似性だったなんて、
嗤うに嗤えないが、

何故かこいつが
死を目前にして迫って来るのだから面白い。
もしかすると
４枚の頭蓋骨を重ね合わせる方法が、

クライン体

勿論ユークリッド空間で実現するには
《4次元と曲率0とすると5次元が必要》と
テキストに書いてあるのを充分承知しての
試みであったのだが。

当然仙人の卵のそのまた卵みたいな
青臭い大学生が、如何なる試行錯誤を重ねようが、
クライン体である４次元の十字帽子を
作ることは出来なかったのは言うまでもない。

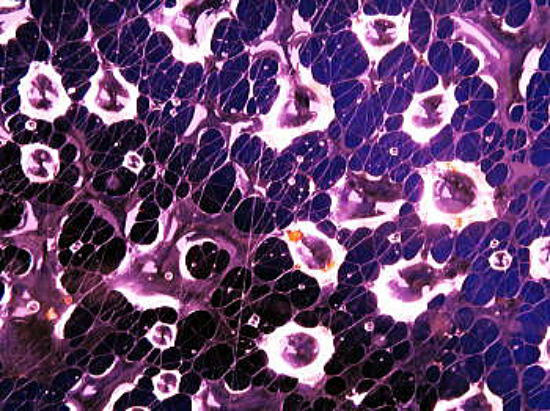銀河が暗黒物質に沿って移動

*ゲート前の森が道に張り出し*	*枝伐り開始*	この境界も表裏の区別も持たない（2次元）曲面のクライン体に見つけられるのでは、なんぞと慮るのであるから捧腹絶倒せざるを得ない。さてさてこのポンコツ老い耄れ見習い仙人は、どうやって大泉門を手に入れるのでしょうかね！　お手並み拝見といきましょうか？
*弟子入り志願者* さて小倉山の頂にさえも達することが出来なかった弟子入り志願者は、その後自己嫌悪に陥りながらどのような決意をしたのであろうかと、テロリストあっらーの一撃を放ってみた。自己嫌悪が本物なら、 ≪躍動する自由への径≫の輪郭くらいは描けるのではとの一撃であったが、相も変わらずの判断の甘さに、	*これ、大紫蝶の餌の臭木では！*	*貴重な樹だが伐らねば*

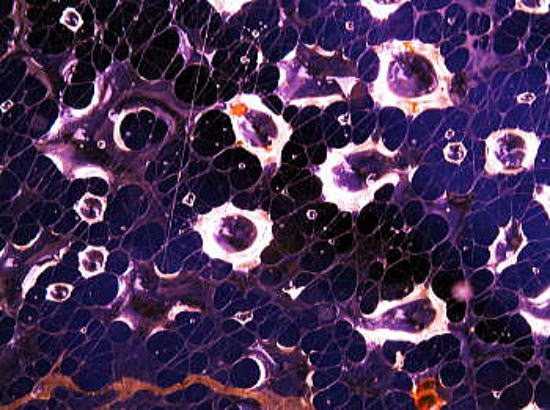銀河とシナプスは心象の絵師

頂への途は、
とても４枚の頭蓋骨を激痛に耐えて重ね合わせてまで、
アプローチしたい≪躍動する自由への径≫なんぞではないと、
知っていて尚、

意識だけは生命讃歌の世界で戯れたいのだ。
そんなら刺さった矢を抜いて楽にしてあげねば！
あっらーの気まぐれな独白なんぞ、
忘れておしまい！

弟子ではなく仙人が自己嫌悪に
陥ったのであるから話にならん。
一撃を喰らい、慌てふためき尻尾を巻いて
一目散に逃げ去る弟子にとって、

山巓とは観るものであって、自らが達する領域ではないと
自己認識しているからこその登頂願望であって、
意識のお遊びでしかなかったのだ。

１つ１つの銀河に込められた想いは？

*茗荷がにょっきり*	昨日のコメント記載後、速攻で《「境界を部分的に繋げて円柱を作ると、円柱の内と外が出来るが」は、ちょっと説明不足で乱暴なのでは！》とのメールあり。うーん、其処まで読み取る繊細で敏感な数学的感性を持つ弟子も居たかと嬉しくなって、昨日の補足をちょっと！	*銀のクロッカスみたい！*
確かに２次曲面の境界を主語にしておきながら、突然円柱が出て来るなんぞ乱暴極まりないね。ほんなら平面だけで話しを進めよう。　１次元の点を同じ方向に１単位（ｃｍでもｍでもいい）動かし、単位１の１次元の線分を作る。次にこの線分を線分の垂直方向に１単位移動すると２次元の正方形が出来る。	*でもオクラの美しさにはね*	この正方形の面の境界である４辺をそれぞれa,b,c,dとする。対辺となるaとcの境界を繋げると円柱ができ、 bとｄが円柱の境界である円となる。若しこの４辺の境界をa,bとc,dで張り合わせると３角形の球と同じ閉じられた空間が出来る。観かたを変えれば４つの頂点を１つに重ねる動作であり、それは正しく４枚の頭蓋骨を大泉門に重ねる動作と同じではないか！
*あれっ！突然夏水仙が！*	*ゲート前の伐採した臭木の花*	*夏水仙が咲きました！*

蜘蛛の巣の雨粒に潜む大泉門
８月２日（火）雨　書斎テラス

一方境界の対辺を繋げて出来た円柱の上下の境界である円のbとｄを繋げると、
閉じられた空間であるドーナツ型のトーラスが出来るのである。さて問題は此処から先である。
この正方形を面と垂直方向に１単位動かすと立方体が出来るが、これは２次曲面による閉じられた空間であり、
位相空間では正方形の４辺の境界をa,bとc,dで張り合わせた閉じられた空間と同じである。

この立方体を更に
立方体に対して垂直となる
４次元方向に１単位移動すると
正８胞体とも呼ばれる
１６個の頂点と３２個の辺を持つ、

4次元超立方体の3次元投影図
（wikipediaより）

４次元超立方体が生まれるが、
勿論我々の世界で
この超立方体を
目にすることは出来ない。
これ何だか蛇足で
必要無かったかな？

*原野へ出発！*	*先ずは入口から*	≪認識の総てが消滅する前に、もう一度だけ命の頂点に立って、生命讃歌を高らかに謳い上げる雪の姿をとどめておきたい≫ 　そう願っていたら諦めていた蜩が、夜明けと共に謳いだしたでは！
昨日の梅雨明けで碧空が広がり始めた高芝山上空に、幾重にも連なるカロスキューマを描いてその音色のなんと麗しいこと。麗しく甘い音色はゆっくりと山荘を包み込み、揺れながらロンドを舞う。	*P2峰ルートまで数百ｍ*	*此処からは２台の草刈機を使い分けて*

幾重にも連なるカロスキューマを描くアポロン
　８月２日（火）　　ガニメデ天窓のファンタジー

繰り返される波動にするりと異なる楽想が忍び込み、シンフォニーは終楽章を迎えるかと思うと、
境界aは一度捩じられ逆方向となった境界cと重なり合い、
深く繋がりプロローグとエピローグを喪失し、メビウスに変身し、際限もない悦楽に墜ちる。
残された境界bとdも、幾重にも連なるカロスキューマを描く音色に抱かれて結合し、
際限もない悦楽を夢見るが、一度捩じられてしまったメビウスの境界は
最早３次元で閉じることは出来ない。　

赫奕たる儀式の果てに

そう、人間は生まれた瞬間に、
生み出された社会の体制、価値観に支配され、
そのボールの内から逃れることは出来ないけれど、
メビウスの帯の境界を閉じてしまえば、
何の抵抗も無くボールの外に飛び出せる。

そして何食わぬ顔して、
再びボールの内へ戻って来ることも出来る。
と云うよりか、ボールの内で動けば最早そこは
内も外も無い境界の無い世界。
従って生まれた瞬間に、生み出された
閉塞社会の体制、価値観なるものは存在しないのだ。

あー、残された境界bとdが狂おしく重なり合おうと、
求めていたカロスキューマは、
それだったんだね！

ほら、《4次元と曲率0とすると5次元が必要》だと
昔、位相空間学で学んだろう。
３次元で境界の殆どは重ねることが出来るけれど、
最後にどうしても重ねられない部分が残ってしまう。

しかし若し残された境界bとdを
深く結合させることが出来れば、
境界の無い閉じられた２次曲面でありながら、
内も外も無い自由に開かれた世界が出現するんだ。
ボールの内部に閉じ込められた人間が、
全く自由に何の障害も無く外の世界に出入り出来る。

山稜を突き破って


	その１２９の１ー２０１６年　　葉月