その１４１の２ー２０１7年　　葉月

仏陀生前の教説アビダルマと媾う相対性理論 アンネ薔薇の花芯で媾う豆黄金虫 ≪ あのーカオちゃんにではなくて豆黄金に訊いてるんだけど？ふーん、やっぱ読めないんだな豆黄金め。 こうなると向日葵の特別講義は何処へやら、カオちゃんの自由研究なんてとても出来そうもありませんね！≫ 勿論これが豆黄金への苛烈な侮辱であり、最大の挑発であることは云うまでもありません。 ぎっこんギッコン、アビダルマと名付けられた豆黄金に圧し掛かり、 横腹に５つの白い毛を靡かせ、 恰もアインシュタインにでもなったつもりで、もう一匹の豆黄金が叫ぶのです。 ≪阿毘達磨はミンコフスキー空間じゃ！≫

桃は過去光円錐ミンコフスキー空間図 物体の速度，加速度，運動量とエネルギー，力と仕事は 適当に定義を改めてこの空間内のベクトルとして， 電場と磁場は反対称テンソルとして表現。 こうして作られたのがミンコフスキー空間。 どう狂ったか、仙人め、 このミンコフスキー空間を、玄関ニッチに鎮座まします ヒマラヤ瑪瑙の壺と 採れたての桃で表現できないかと、 ウロウロうろうろ。 仙人って、ほんとうに閑なんだな！	ロシア（リトアニア）生まれのユダヤ系ドイツ人数学者 ヘルマン・ミンコフスキーは チューリヒのスイス連邦工科大学教授 (96～1902) 時代 A.アインシュタインを教えていた。 その後アインシュタインの特殊相対性理論は、 ミンコフスキー空間として幾何学表現された。 四次元の時空を用いて 対称な双線型形式の未来光円錐、過去光円錐を描き、 三次元空間の事象を，ミンコフスキー空間の1点として表わした。
	未来光円錐が現れる 非退化で対称な双線型形式を持つ実ベクトル空間

y軸を軸にして回転させると 円錐が出来る。 3次元となるｚ軸を入れると 右下図のような半径ｒの円錐方程式 ｚ２＝ｒ２＝ｘ２＋ｙ２となる。 絶対値｜x｜のグラフ そーら簡単だったろ！ 思い出せばあとは簡単。 この定数であるｒを変数にして その座標軸をｚとすれば円錐方程式の いっちょ上がり。 つまり ｚ２＝ｒ２＝ｘ２＋ｙ２ 此処で思いっ切りぶっ飛んで 一気に4次元の世界線 なるものをぶち込んで ミンコフスキー空間を イメージしようってんだ」 ≪あれれ、ｘ君とｙ子さんは どうしちまったんだい？≫ すっかり仙人の遊び道具にされて しまった桃が訊ねると 仙人は澄ました顔して云ったとさ。 「２人の速度，加速度，運動量と エネルギー，力と仕事は 適当に定義を改めてだな、 この空間内のベクトルとして表わし、 ２人が周りに及ぼした 電場と磁場は反対称テンソルとして、 表わせば、どうだ ミンコフスキー空間のいっちょ上がり！」 いやはや懼れ入りました。 しかしここまでしっちゃかめっちゃか になるとは 仙人の終焉は最早、限りなく近いぜ！

混沌仙人が閑に任せて何やらぶつぶつ。 「≪特殊相対性理論がミンコフスキー空間として幾何学表現された≫ なんて云われた途端ビビっちゃうだろ。 何ツ―ことはないんだよ。 滅茶苦茶脱線して例え話をすると、こんな具合さ。 ｘ君とｙ子さんが恋に落ちて、ｘ君が一定の速度で変化すると ｙ子さんも同じ速度で変化するなら 2人の関係はｙ＝ｘと数式で表現してもいい。 しかし恋をしてるのｘの負への変化は、 何故かｙにとっては総て良い事、正の変化に観える。 となると2人の関係はｙ＝｜x｜となる。 あーもう此処で解んないって！ 絶対値｜x｜てのはｘがマイナスになってもｙはプラスになると云うだけの話し。 それを解り易く左図のようにすると、代数が幾何学表現された訳。 こいつをｙ軸を軸に回転させると円錐が出来るだろ。 ｒ２＝ｘ２＋ｙ２　この数式、何処かで観たことないかい？ 高校の数学で習った筈。 原点０から半径ｒの点の集合、つまり円さ。 思い出したかい？ 駄目だって！そんならちょこっとだけ特別講義じゃ！ 中三で習ったピタゴラスの定理・別名三平方の定理から 簡単に導けるよ。左下の直角三角形で 定理をそのまま使えば半径ｒの円方程式の出来上がり。

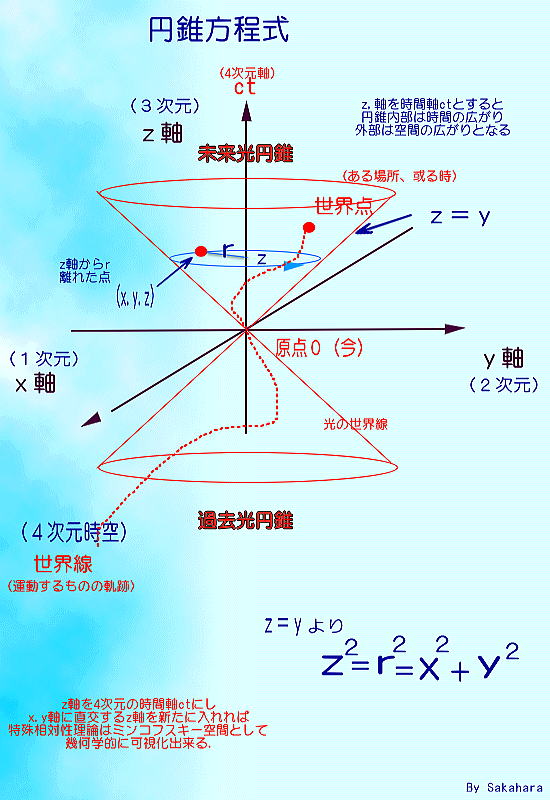ミンコフスキー空間の4次元方程式 c2t2＝x2＋y2＋z2 （cは光速tは秒）

ミンコフスキー空間として可視化出来るか テラス上の熊蜂の巣を襲撃し解体 テラス上の２階軒下に造られた円錐状の熊蜂の３次元巣を解体し、２次元状に並べ仙人のモノローグは続く。 「ミンコフスキー空間なんて、とっ捉まえて３次元にしてしまえばこんなもんさ。 線の世界１次元から面の２次元世界は観えない。 同様に２次元から３次元世界は観えないのだから、当然ながら我々の３次元世界から４次元は観えない。 これを可視化するには次元を１つ下げて、 例えば3次元の空間図を１つ下の２次元の面に描けば、視覚的に実感できる。 となると４次元ミンコフスキー空間を可視化するには、3次元空間に幾何学表現すればいいのだ。 そこで円錐方程式に御登場願うわけだ。

軒の熊蜂を夜襲攻撃！	蜂の卵がびっしり	桃で描いたミンコフスキー空間図を 観てごらん！ 中央にある平面に座長軸が 入れられて空間と書かれているだろ。 考えてみれば変だろ？ 平面なら2次元じゃないか？ これが味噌なんだ。 これを空間だと思えれば、あとは簡単！ 平面に垂直な直線ｚ軸を入れて 3次元を造った様に、 この平面の3次元に垂直な４次元の 直線、座標軸ｃｔを入れればＯＫ。
蜂の子の頭が金色を発しているでは！
3次元の図形を１次元の直線で切ると 切断面は2次元平面に なるだろう。 その平面は垂直方向の3次元と 2次元の境界でもある。 ならば4次元を切るとその切断面は、 どうなるのか？ 4次元と３次元の境界は何処に？ 実はそれが光の世界線なんだ。 つまりこの円錐の内側は、 4次元で外側は３次元の空間なんだ」	真珠の卵が数段の層を成す	化学兵器で蜂の動き封殺

四次元空間に表現される質点の運動の軌跡。物理的な事象は、ある場所、ある時間に起こるが、
これを時間・空間を一体化した四次元空間（ミンコフスキー空間）で表すと、一つの点となる。


「 何故4次元の座標軸に光速のｃが出て来るんだい？」
頭から黄金の光を発しながら仙人に問い掛ける熊蜂の幼虫。
≪阿毘達磨はミンコフスキー空間じゃ！≫と
叫んだアインシュタインらしき豆黄金虫の謎解きは、いつになったら出来るんでしょうな！

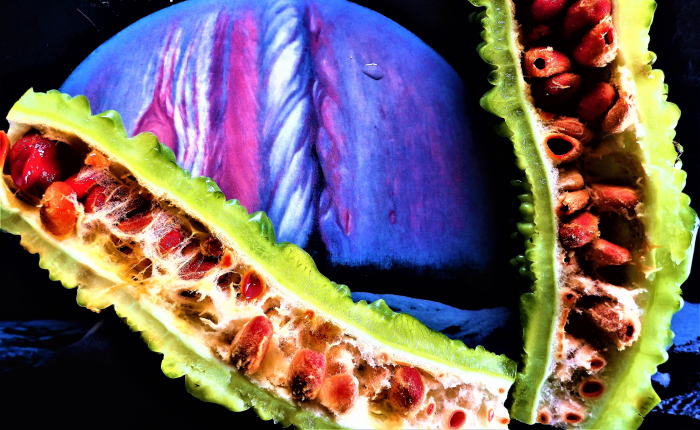ゴーヤーの世界線の彼方に濡れる木星

「≪円錐の内側は、4次元で 外側は３次元の空間なんだ≫　だって！ 光の世界線を超えたら３次元の空間が 現われるだって！ よくもそんな出鱈目が云えるもんだ。 さては混沌仙人の脳はいよいよ 混沌として、機能しなくなったな！ 円錐の内側が４次元なのは確かだが、 世界線を超えて３次元空間に 遭遇するなんて有り得ない。 いいかい、世界線を超えると云う事は 光速を超えると云う事で、 新たな次元の軸が必要になるんだ。 いや次元すら超えた 因果律の破綻した世界に なってしまうと云うこと」

しゃしゃり出てきたのは 採れたばかりのゴーヤーでは！ 煩いので包丁で 真っ二つに切り裂いたら おりゃ、世界線らしき科を造って 宣うでは。 さてはゴーヤーの奴、 特殊相対性理論の微視的因果律に 気づいているな。 世界線の外側、つまり光速を超えた世界が 因果律の破綻した空間であると 何処かで聞きかじって、 仙人の無知を嘲笑っていると云う事か！ はて、因果とは確か仏教用語。 ≪この世のすべての事象は、原因の中に すでに結果が包含されている≫ とか述べたのは 仏教以降に再編成されて出来たヒンドゥー教の 正統バラモン教の一派。

花器は世界線を超えた５次元空間の座標軸か！

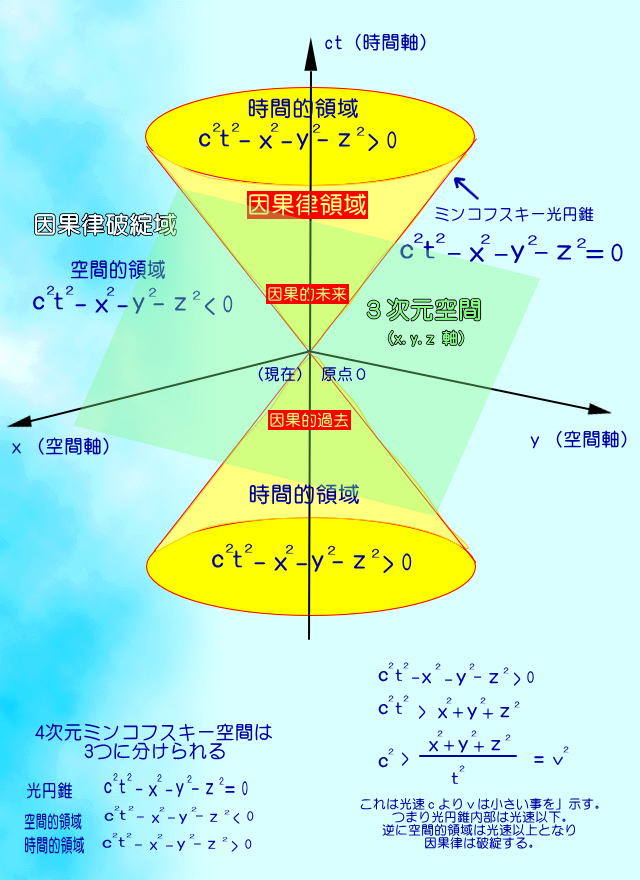「ゴーヤーの知ったかぶりに タジタジとなった混沌仙人は、あれやこれや 資料を漁り、３日間も掛けて 作り上げたらしいミンコフスキー光円錐の図。 それでは仙人の言い訳がましい ご高説を伺ってみましょうか！」 と再び出てきたのは熊蜂の幼虫。 （見易い様にここから英字は大文字に） うーん、そうだな最初にこの4次元軸ＣＴの 入れ方については、 Ｚ２＝Ｘ２＋Ｙ２と円の方程式Ｒ２＝Ｘ２＋Ｙ２と 同じやり方だと解るかな！ つまりＸＹ座標の平面上に円を載せ Ｒ２＝Ｘ２＋Ｙ２　半径Ｒを変数にして、 Ｒ＝Ｙを保ちつつ そのまま平面と直交するＺ軸方向へ 持ち上げれば円錐方程式の出来上がり。 同じことを3次元空間上に、 ４次元時間軸ＣＴを作ればいいんだ。 問題は何故時間軸をＣＴとするかなんだけど、 納得いかないよね。 時間軸だからＴで良いじゃないかって！ その通り、Ｔで良いんだ。 Ｃは光速で定数、変数はＴだけなので ４次元軸はＣＴとなっていても 時間軸であることは間違いない。 原点の現在である事象が起きると その影響は上の円錐・因果的未来にのみ及び、 現在に影響をしているのは 下の円錐・因果的過去のみと云う 時間的領域が因果の世界である。 ＝、>、<の意味が解んないって！ それじゃ中学生に戻って ちょっと復習する？

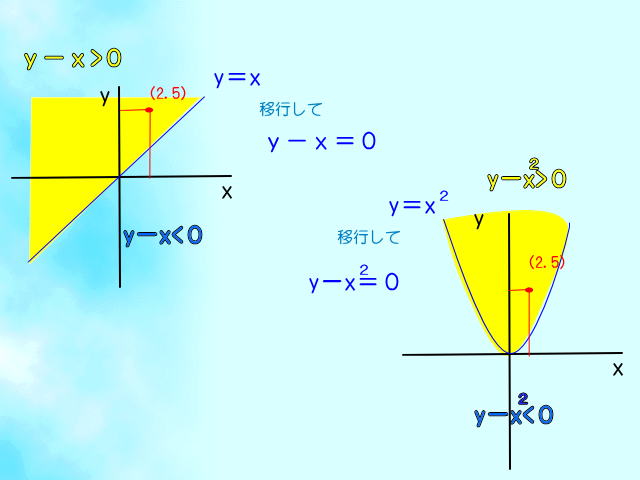
ほら、思い出しただろ！ Ｙ＝Ｘの場合は Ｘを移行してＹ－Ｘ＝０にすると この方程式を満たすＸ，Ｙの値は 総て45度の直線上にある。 Ｙ－Ｘ>０を満たすＸ，Ｙの値は総て 黄色い領域になるだろう。 Ｙ－Ｘ２>０にしても同じ。 因みに点（２．５）を代入すると Ｙ－Ｘ>０では５－２＝３で０より大きい。 Ｙ－Ｘ２>０では ５－２２＝５－４＝１でで０より大きい。 ミンコフスキー空間では 4次元方程式が０より大きい領域は 上図のように黄色い部分になると これで納得出来たかな？

お馴染みオクラでーす	知ってましたか？ オクラって ハイビスカスなんです 閑を持て余した仙人が 次にやって来たのがオクラ畑。 「うーん、いつ見ても オクラの花は美しいのー！」	美しいですよね
クリームの絹が光を 吸い込んで、 花弁が花芯の翳を暴こうと 企んでいます。	５稜の実を着ける 粘り気の正体は、ペクチン、アラピン、 ガラクタンという食物繊維で、 コレステロールを減らす効果が あるんだって！ その上、ビタミンA、B1、B2、C、 ミネラル、カルシウム、カリウムなどが 含まれるから便秘や下痢を防ぐ 整腸作用もあるとか！	この黒ずんだ５つの赤紫が やがて５つの稜になって ぬるぬるした オクラの実になるんだ。
そーら、柱頭が５菱に		花弁の根元にも花弁が

花芯の翳が ５つの稜を成し 稜の内部に 虚空を生みだし、

翡翠の耀きを放ち あなたは こんなにも 美しかったのですね。

更に桃が続々と大進撃して山荘にやって来た！ 山荘は何処も彼処も桃だらけ！ 時空の旅をしている。 湯川秀樹がノーベル物理学賞を受賞した１９４９年には５歳であったのだから、 幼い仙人の記憶媒体を幾らリセットしてみたところで、何も出て来はしない。 ≪物心ついてからほとんど口を利かず、面倒なことは全て「言わん」の一言で済ませていたため「イワンちゃん」とも呼ばれていたが、 案外『イワンのばか』から取ったのではないかと自分で考えた時期もあった≫　 と本田靖春『現代家系論』湯川秀樹には書かれている。

玄関を開けて吃驚！	ビーナスにも飾ってあげよう！	誰ですか又また桃を持ってきたのは？
そう云えば日本で最初の ノーベル賞受賞者が、親からも能力を 低く観られるような 普通の少年であったことが、 当時の敗戦直後の 日本の少年たちに 大いなる希望を与え、 日本中が沸き立った様な 微かな揺らぎくらいは、 覚えているかも知れない。 そこで夜明けの ガニメデに昇って森と対峙し、 とっくにお蔵入りし錆びついた		記憶媒体の鍵に油を差し、 嘗て夢中になって漁った 中性子や陽子の知識を追う旅を 愉しむことにした。 残されているのは 知識の上澄み液だけで、 森全体は観えるが 個々の事象は殆ど失われ、 １本１本の木々が実に不鮮明。 失われてしまった 時空の宝石箱を開き、 １本１本の輝きを追うことが愉しい。 巨大恒星の死を目前にした 中性子星が観えてくるのである。
キーボードにも		桃の演奏会じゃ！

すっかり種だけになって！

≪夏休み自由研究で眼を キンキラさせている 小学１年生のカオちゃんの為に 特別講義じゃ！≫ と向日葵が始めた講義が、 山荘の出しゃばりで 頭すっからかんの山荘住人達によって ７月からだらだらと繰り広げられ、 最後は中学数学の Ｙ－Ｘ２>０で 終わりか！ ほら向日葵だってもう種だけに！ お粗末な自由研究で終わってなるかと 何やら３０年前・１９８７年の 夏休みの自由研究を 引っ張り出そうと、 ごそごそ探し始めた仙人。

鬼灯と珊瑚と向日葵が夏の終わりを